

具体问题就是已知矩阵w,该矩阵映射唯一的多个输出。优化使得矩阵w的模最小时,该矩阵映射的多个输出误差最小(误差指优化前的输出与优化后的输出,每一个输出都是独立的)
这些方法都是可以用的,没有任何问题。
可以利用这些方法对多目标优化问题进行预处理。比如预测可能的最优前沿。
也可以利用强化学习来自适应地选择当前最优操作。
根据题主的问题描述,我的理解其实是题主想知道怎么用深度学习或者强化学习求解多目标的问题。而不是已有答主所侧重的优化问题。
令人开心的是,2017年,Neuro Computing有一个special issue就是专门针对multi-objective reinforcement learning。其中一共有七篇文章对多目标强化学习进行了研究。 而今天我们主要对其中的一篇文章进行讲解。
今天要讲解的这篇文章的标题是“Multi-objectivization and Ensembles of Shapings in Reinforcement Learning”。主要是通过reward shaping和集成的方法来进行多目标的强化学习。
Ensemble Techniques in Reinforcement Learning
Wiering和van Hasselt,第一次在强化学习中引入了集成技术。他们是通过几种不同的强化学习算法从相同的经验中并行学习,从而得到不同的模型来进行集成。而集成的方法是投票制。
但是在本文中,作者的集成技术并不是将几个不同强化学习算法所构成的模型进行集成,而是利用不同的reward来构成不同的模型,从而进行集成。这其中不同模型的网络架构很可能是一致的。我们将这个集成过程用下面的公式进行描述。其中,wi表示对每个参与集成的模型的权重,而pi表示每个模型输出的概率分布。
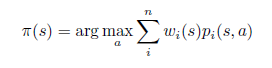

而针对具体集成的方法,有以下几种方法可以选择:
Linear: 直接对每个模型输出的概率分布进行线性组合,而每个wi就是根据经验选择每一个模型的重要程度。 Majority Voting: 每一个模型自己选出来最合适的action,然后计算每一个action的得票数,从而来进行决策。 Rank Voting:每一个模型对action进行排序,最后将每一个action的排序号加起来,最终最小的那个action就成为当前的策略。 Confidence-based:每个action对应的不是一个具体的概率值或者Q值,而是一个分布。刺种方法比较复杂,想要知道更具体的做法可以参考文章“Combining multiple correlated reward and shaping signals by measuring confidence”
Reward Shaping
虽然reward shaping和求解多目标问题没有太多关系,但是也是文章中介绍的重点,在这里也提一下子吧。此处的reward shaping指的是在本身给定的环境报酬的基础上,通过shaping function F来提供额外的报酬,从而整合一些启发式信息的方法。
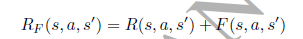
好啦,以上就是利用集成的方法来实现多目标强化学习的过程啦,更多的多目标强化学习方法可以参考neuro computing的special issue喔!
文章源码下载地址:点我下载http://inf.zhihang.info/resources/pay/7692.html
多任务学习之mmoe理论详解与实践
书接上文,在前一篇文章 快看 esmm 模型理论与实践 中,我们讲到MTL任务通常可以把可以分为两种: 串行与并行 。多个任务之间有较强关联的, 例如点击率与转化率,这一种通常我们可以使用 ESMM 这种串行的任务进行 关系递进性与相关性 建模。而对于多个任务之间相对比较独立的,例如点击率与用户是否给出评论的评论率,通常可以选择 MMOE 这种并行的任务进行 相关性与冲突性 的建模。
MMOE 模型全称是 Multi-gate Mixture-of-Experts, 该模型由 Google在 2018年 KDD 上发表的文章 Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts 中提出的。
MMOE 模型本身在结构上借鉴了以前的 MOE 模型,但又有一定的创新, 它可以说是提出了一种新的 MTL(Multi-Task Learning) 架构,对每个顶层任务均使用了一个 gate网络 去学习融合多个专家对当前 Task 的权重影响, 在很大程度上调节缓解 多目标任务相关性低导致的准确率低 的问题。
本文,我们主要对mmoe模型进行理论与实践过程的阐述...

说到 mmoe 模型,我们一般总是会把它横向的和阿里巴巴提出的esmm模型进行对比,而纵向的和最初shared-bottom、moe进行对比,这里我们分别也从横向和纵向对比展开。
首先是 esmm模型 ,和mmoe一样 , 它也是一种(Multi-Task Learning,MTL) 模型。esmm 模型相关内容,可以去这里 快看 esmm 模型理论与实践 查看。但是上文我们也说了, esmm 我们建模的是一种串行的任务,任务关系之间有 递进 的性质。而mmoe则不要求两个任务有递进的关系。
在这里,我们之所以一直强调esmm模型适合建模递进任务,我们可以从esmm的损失函数可以看到:
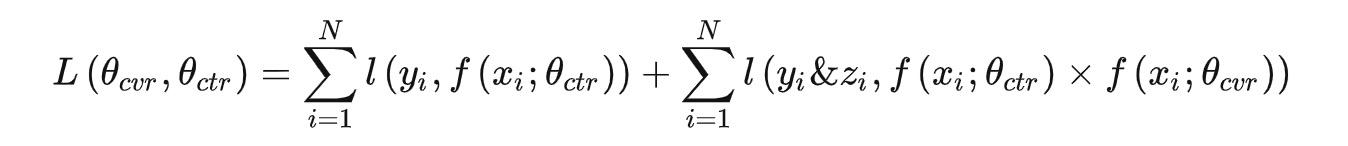
, 我们可以重点关注下他的CTCVR损失。
而建模的pCTCVR 的 概率建模逻辑 又可以这样表示:

读过上面介绍esmm文章的同学就可以看到,pCTCVR 任务的核心是: 我们站在曝光的前提下,不知道点击与否,不知道转化与否,这个时候去预估点击并且转化的概率。
如上所述,CTR 任务和 CVR任务 都是进行分类模型的0/1概率预估, 用到的特征相似, 场景也相似, 任务相关性非常高。并且,该模型使用的业务场景也要求了在曝光后,item先被点击才会有转化,没有被点击就压根谈不上转化了,这是一种严格的递进关系。同时CTR与CVR两者的概率相乘有着明显且理论正确的业务意义。
我们从 上篇文章 里也了解到: esmm 模型从任务的根本“损失函数”上就保证了这种曝光前就去预估点击且转化的概率建模逻辑。 如果任务本身没有 严格递进且高度相似相关,那我们这里的损失建模就没有意义了。
或则,我们也可以改变esmm模型的损失函数(去掉严格递进且高度相似相关的关系逻辑),用它去建模一些不那么相关的 multi-task 任务,毕竟是DNN模型,只要你能把跑起来,总是可以predict出一个结果的。但是如果损失函数有了大的本质上的改变,esmm模型就失去了它的精华,那这个模型还叫esmm模型吗?

而对于本文介绍的MMOE模型,我们对他的样本就没有那么多的要求,它可以进行并行与冲突性建模。当然,没有那么多的要求不是没有要求,至少两个任务的样本和特征是能共享的吧,业务能够有交叉的吧,最重要的是多个任务的损失融合后能找到一定的优化意义的吧。
例如:视频推荐中,我们有多个不同甚至可能发生冲突的目标,就像多个task是去预估用户是否会观看的同时还希望去预估用户的观看时长,同时预估用户对于视频的评分。这中间就同时有 分类任务 和 回归任务 了。
这里我们引入一些 任务相关性衡量 的简单介绍:
我们知道: Spearman相关系数仅评估单调关系,Pearson相关系数仅评估线性关系。例如: 如果关系是一个变量在另一个变量增加时增加,但数量不一致,则Pearson相关系数为正但小于+1。 在这种情况下,Spearman系数仍然等于+1。
我们这里说的 两个任务的相关性,可以通过 两个任务的label 之间的 皮尔逊相关系数 来表示 。假设模型中包含两个回归任务,而数据通过采样生成,并且规定输入相同,输出label不同,求得他们的皮尔逊相关系数,相关系数越大,表示任务之间越相关,相关系数越大,表示任务之间越相关。
说到 mmoe,因其一脉相承血浓于水,不得不提到 shared-bottom与moe 这两个模型。这里,我们通过对比三种模型的 异同 来 逐渐 引出 mmoe 模型的特点。 闲言少叙,上图:
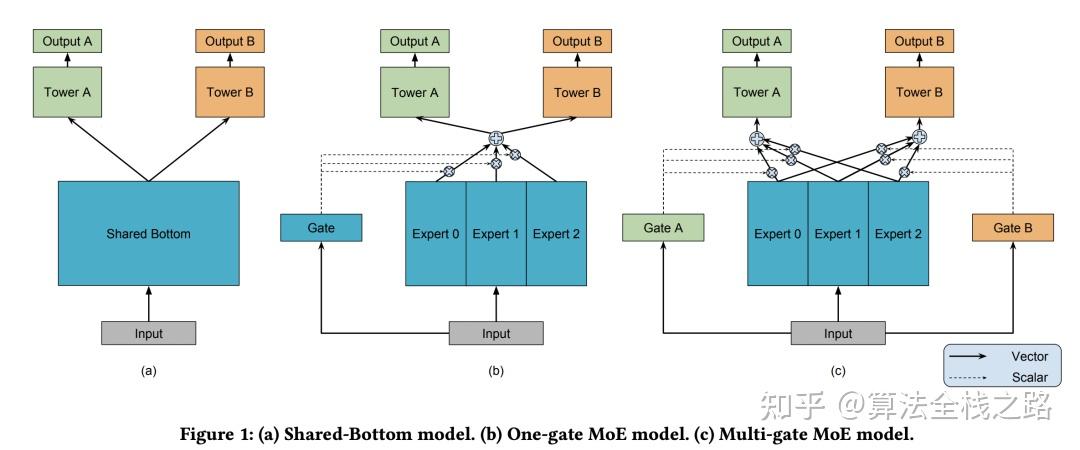
从上面图中,我们可以看出:在三个图(a,b,c)中,从下往上分别是模型的输入到输出的流程。
如上图a所示,假设我们的模型中有N个任务,则在上层会有K个塔 (图中K=2)。其中,上层的每个塔对应一个特定任务的个性化知识学习,而底层的shared-bottom 层作为共享层,可以进行多个任务的知识迁移。
注意:输入的input在我们的理解里,已经是各个sparse 或dense特征得到embeding 并且拼接之后的结果,理论上是一个[batch_size, embeding_concat_size]的tensor。
如上图所示:图a 是原始的 shared-bottom 结构,2个 task 共享隐藏层的输出结果, 输入到各自任务的tower, 一般的 tower 也就是几层 全连接网络 ,最后一层就是分类层或回归层,和常规的分类回归任务没有什么区别。
图b 就是最初版本的 moe 网络 ,我们从图中可以看到有个gate网络,并且只有一个gate门控网络,同时图b中有三个专家网络。
我们可以看到:gate门控网络的输出维度和专家个数相同,起到了融合多个专家知识的作用。融合完了之后会有一个公共的输出,该相同的输出分别输入到上面2个tower中。
常规网络中,gate网络和tower网络均是几层 全连接网络,只是最后的输出看情况考虑维度以及是否需要添加 relu 与 softmax 函数等。
这里要注意一点就是: 我们的input是分别作为各个专家和gate门控网络的输入,各个专家和门控网络分别独自初始化以及训练。gate网络的输出的各个维度和各个专家的输出进行加权求和,得到一个综合专家维度的输出,然后相同的输入分别输入到上面两个不同的任务中。
这里我们从网络结构上可以明显看到MOE和初始网络的区别,多了一个多专家加权融合的门控网络,使得各个专家学习到的知识进行平滑的融合,可以让模型训练的更好。

图c 就是我们本文要重点介绍的 mmoe 网络了。 mmoe 说白了,就是一种新的MTL网络架构的创新。mmoe 实际上就是 多个门 的 moe 网络。 输入多个专家的过程和moe无任何区别,这里唯一的不同是对每一个任务有一个门控网络。
mmoe和moe最大的差别就在于输入上面任务的输入。 moe的任务tower输入的是经过同一个门控网络加权过的多个专家的输出,是相同的一个embeding。 而mmoe 的任务tower 输入的则是经过自己任务特有的门控网络加权过的多个专家的输出,对于不同任务是不同的。没有明显增加参数,却对网络的学习起到了重要的影响作用。
通俗理解 : 我们网络中的每个专家都是可以学到一些关于多个任务的各自的专业知识,而我们用多个门控网络,就相当于起到了一个Attention的作用。就例如: 我们使用一个多目标任务网络去预估一个人分别得感冒和高血压的概率,我们现在有多个专家都会相同的这个病人进行会诊,但是每个专家各有所长又各有所短,这个时候,我们就通过一个门控网络去自动的学习对于某种病情应该多听从哪个专家的意见,最后对各个专家的意见进行加权求和之后来综合评定这个人患某种病的概率。
让每个专家发挥出各自的特长,是不是更有利于我们实际的情况呢?
而开篇所提到的mmoe网络的 冲突性建模能力 也就来自于这多个门控网络对于多个任务可学习的调控能力。多个专家加上多个门控网络,不同任务对应的门控网络可以学习到不同的 Experts 组合模式,模型更容易捕捉到子任务间的相关性和差异性,能够使得我们多个任务融合的更加平滑 ,最终打分得出的结果也更加能够动态综合多个专家的特长与能力,得出一个更有益于我们业务目标的结果。
前文我们已经介绍过, mmoe网络的提出主要就是提出了一个新的MTL架构。所以上文中,我就没有在引入一些晦涩难懂的公式,而是全部采用了文字说明的形式来下进行阐述,希望能似的读者看起来更丝滑一些~

其实相对于esmm模型,mmoe模型更好理解,构造样本等也更加容易。
但是仍然有一点就是: 我们在使用tensorflow 或 pytorch 实现网络的过程中,多个专家以及门控网络的输入输出维度对应上有一定难度,有隐藏的暗坑在里面。不过这些在上文中,我也大概以文字的形式说清楚了,后面分享的代码源码我也根据自己的理解进行了详细的注释,希望对读者的理解有帮助哈~
在实际使用mmoe的过程中,有同学会遇到:训练mmoe的过程中,发现多个gate的输出过度偏差 ,例如:(0.999,0.001)情况。 这一种情况初步感觉还是:**(1)** 网络的实现有问题,需要去排查下各个专家网络以及门控网络的初始化值有没有问题。 (2) 去排查下两个任务的标签情况,是不是两任务的标签呈现比较多的极端情况,也可以采用上面介绍的任务相关性衡量办法看一下两个任务的相关性。 在输入相同的情况下在网络理论上不应该出现这个问题我在使用过程中并没有遇到,所以只能给出一些猜测的解决方法...
当我们遇到两个任务的目标差异特别巨大时,例如:预估视频点击率与观看时长。这个任务我们应该直觉上就觉得标签的差异太过于大了,时长的label最好能够进行一定的处理。例如log处理。
log函数有着优秀的性质,经过log处理后目标会削弱量级,数据也会变得更符合正态分布,同时loss也更小和稳定 。loss的稳定对于多任务模型学习和训练来说是至关重要的,它影响着多个任务根据loss更新的梯度,最好我们能够把多个目标的loss加权重调到同一量级,对这种差异比较大的问题总是能够起到缓解作用的额
同时在进行mmoe网络设计的过程中,我们不仅可以使用多个任务有共享的专家(官方版本),其实我们也可以给每个任务加上各自独特的专家进行组合学习,期望模型可以学习到各个任务之间的个性与共性。
另外, 我们可以将mmoe 作为一种复杂的DNN layer ,我们可以在网络中叠加多个 mmoe layer , 实现一些比较复杂的网络来学习一些比较复杂的多目标任务。
talk is cheap , show me the code !!!
哎, 终于再次写到代码时光了!
对于mmoe 模型,才开始看源码到最后理解花了挺长时间,中间主要的时间都花在了实现的时候专家网络和多门控网络的输入输出维度对应上。下面的代码注释均写的比较详细,看的过程中,如有任何问题欢迎公众号留言讨论 ~
@ 欢迎关注微信公众号:算法全栈之路
# coding:utf-8
import numpy as np
import os
import argparse
import tensorflow as tf
import log_util
import params_conf
from date_helper import DateHelper
import data_consumer
from mmoe import MMoE
from tensorflow.keras import layers, Model
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.callbacks import Callback
from tensorflow.keras.initializers import VarianceScaling
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
os.environ["CUDA_VISIBLE_DEVICES"]="-1"
import tensorflow as tf
from tensorflow import tensordot, expand_dims
from tensorflow.keras import layers, Model, initializers, regularizers, activations, constraints, Input
from tensorflow.keras.backend import expand_dims, repeat_elements, sum
class MMoE(layers.Layer):
"""
Multi-gate Mixture-of-Experts model.
"""
def __init__(self,
units,
num_experts,
num_tasks,
use_expert_bias=True,
use_gate_bias=True,
expert_activation='relu',
gate_activation='softmax',
expert_bias_initializer='zeros',
gate_bias_initializer='zeros',
expert_bias_regularizer=None,
gate_bias_regularizer=None,
expert_bias_constraint=None,
gate_bias_constraint=None,
expert_kernel_initializer='VarianceScaling',
gate_kernel_initializer='VarianceScaling',
expert_kernel_regularizer=None,
gate_kernel_regularizer=None,
expert_kernel_constraint=None,
gate_kernel_constraint=None,
activity_regularizer=None,
**kwargs):
"""
Method for instantiating MMoE layer.
:param units: Number of hidden units 隐藏单元
:param num_experts: Number of experts 专家个数,可以有共享专家,也可以有每个任务独立的专家
:param num_tasks: Number of tasks 任务个数,和tower个数一致
:param use_expert_bias: Boolean to indicate the usage of bias in the expert weights. 专家的权重是否添加偏置
:param use_gate_bias: Boolean to indicate the usage of bias in the gate weights. 门控的权重是否添加偏置
:param expert_activation: Activation function of the expert weights. 专家激活函数
:param gate_activation: Activation function of the gate weights. 门控激活函数
:param expert_bias_initializer: Initializer for the expert bias. 专家偏置初始化
:param gate_bias_initializer: Initializer for the gate bias. 门控偏置初始化
:param expert_bias_regularizer: Regularizer for the expert bias. 专家正则化
:param gate_bias_regularizer: Regularizer for the gate bias. 门控正则化
:param expert_bias_constraint: Constraint for the expert bias. 专家偏置
:param gate_bias_constraint: Constraint for the gate bias. 门控偏置
:param expert_kernel_initializer: Initializer for the expert weights
:param gate_kernel_initializer: Initializer for the gate weights
:param expert_kernel_regularizer: Regularizer for the expert weights
:param gate_kernel_regularizer: Regularizer for the gate weights
:param expert_kernel_constraint: Constraint for the expert weights
:param gate_kernel_constraint: Constraint for the gate weights
:param activity_regularizer: Regularizer for the activity
:param kwargs: Additional keyword arguments for the Layer class 附属参数若干
"""
super(MMoE, self).__init__(**kwargs)
# Hidden nodes parameter
self.units=units
self.num_experts=num_experts
self.num_tasks=num_tasks
# Weight parameter
self.expert_kernels=None
self.gate_kernels=None
self.expert_kernel_initializer=initializers.get(expert_kernel_initializer)
self.gate_kernel_initializer=initializers.get(gate_kernel_initializer)
self.expert_kernel_regularizer=regularizers.get(expert_kernel_regularizer)
self.gate_kernel_regularizer=regularizers.get(gate_kernel_regularizer)
self.expert_kernel_constraint=constraints.get(expert_kernel_constraint)
self.gate_kernel_constraint=constraints.get(gate_kernel_constraint)
# Activation parameter
# self.expert_activation=activations.get(expert_activation)
self.expert_activation=expert_activation
self.gate_activation=gate_activation
# Bias parameter
self.expert_bias=None
self.gate_bias=None
self.use_expert_bias=use_expert_bias
self.use_gate_bias=use_gate_bias
self.expert_bias_initializer=initializers.get(expert_bias_initializer)
self.gate_bias_initializer=initializers.get(gate_bias_initializer)
self.expert_bias_regularizer=regularizers.get(expert_bias_regularizer)
self.gate_bias_regularizer=regularizers.get(gate_bias_regularizer)
self.expert_bias_constraint=constraints.get(expert_bias_constraint)
self.gate_bias_constraint=constraints.get(gate_bias_constraint)
# Activity parameter
self.activity_regularizer=regularizers.get(activity_regularizer)
self.expert_layers=[]
self.gate_layers=[]
# 在初始化的过程中,先构建好网络结构
for i in range(self.num_experts):
# 有几个专家, 这里就添加几个dense层, dense层的输入为上面传入, 当前层的输出维度为units的值, 隐藏单元个数
self.expert_layers.append(layers.Dense(self.units, activation=self.expert_activation,
use_bias=self.use_expert_bias,
kernel_initializer=self.expert_kernel_initializer,
bias_initializer=self.expert_bias_initializer,
kernel_regularizer=self.expert_kernel_regularizer,
bias_regularizer=self.expert_bias_regularizer,
activity_regularizer=None,
kernel_constraint=self.expert_kernel_constraint,
bias_constraint=self.expert_bias_constraint))
# 门控网络, 门控网络的个数等于任务数目 , 但是取值数据的维度等于专家个数 , mmoe 对每个任务都要融合各个专家的意见。
# 有几个任务,
for i in range(self.num_tasks):
# num_tasks个门控,num_experts维数据
self.gate_layers.append(layers.Dense(self.num_experts, activation=self.gate_activation,
use_bias=self.use_gate_bias,
kernel_initializer=self.gate_kernel_initializer,
bias_initializer=self.gate_bias_initializer,
kernel_regularizer=self.gate_kernel_regularizer,
bias_regularizer=self.gate_bias_regularizer, activity_regularizer=None,
kernel_constraint=self.gate_kernel_constraint,
bias_constraint=self.gate_bias_constraint))
def call(self, inputs):
"""
Method for the forward function of the layer.
:param inputs: Input tensor
:param kwargs: Additional keyword arguments for the base method
:return: A tensor
"""
# assert input_shape is not None and len(input_shape) >=2
# 三个输出的网络
expert_outputs, gate_outputs, final_outputs=[],[],[]
# 专家网络
# 有几个专家循环几次
for expert_layer in self.expert_layers:
# 注意这里是当前专家的变化
# 输入的元素元素应该是整体embeding contact之后的一堆浮点数维度数据。
# (batch_size, embedding_size,1)
expert_output=expand_dims(expert_layer(inputs), axis=2)
# nums_expert * ( batch_size, unit, 1)
expert_outputs.append(expert_output)
# 同 batch 的数据,既然是沿着第一个维度对接,那根本就不用看第二个维度,那个axis的维度数目相加
# nums_expert * ( batch_size, unit, 1) -> 这里 contact 之后,列表里 num_experts 个 tensor 在最后一个维度concat到一起,
# 则最后维度变成了 ( batch_size, unit, nums_expert ),只有最后一个维度的维度值改变了。
expert_outputs=tf.concat(expert_outputs, 2)
# 门控网络, 每个门对每个专家均有一个分布函数.
for gate_layer in self.gate_layers:
# 对于当前门控,[ batch_size,num_units ]->[ nums_expert,batch_size,num_units ]
# 有多少个任务,就有多少个gate
# num_task * (batch_size,num_experts),这里对每个专家只有一个数值,和专家的输出维度unit相乘需要拓展维度
gate_outputs.append(gate_layer(inputs))
# 这里每个门控对所有的专家进行加权求和
for gate_output in gate_outputs:
# 对当前gate,忽略 num_task维度,为 (batch_size, 1, num_experts)
expanded_gate_output=expand_dims(gate_output, axis=1)
# 每个专家的输出和gate的数据维度相乘
# ( batch_size, unit, nums_expert ) * (batch_size, 1 * units, num_experts),因此 1*units
# If x has shape (s1, s2, s3) and axis is 1, the output will have shape (s1, s2 * rep, s3).
# 这里的本质是 门控和专家的输出相乘维度不对,如上面所说,门控维度1和需要拓展到各个专家的输出维度 unit,方便相乘。
# "*"算子在tensorflow中表示element-wise product,即哈达马积,即两个向量按元素一个一个相乘,组成一个新的向量,结果向量与原向量尺寸相同。
weighted_expert_output=expert_outputs * repeat_elements(expanded_gate_output, self.units, axis=1)
# 上面输出的维度是 (batch_size, unit, nums_expert ),对第二维nums_expert求和则该维度就变成一个数值 -> (batch_size,unit)
# 这里对各个专家的结果聚合之后,返回的是一个综合专家对应的输出单元unit维度.
# 最终有多个门控,上面多个塔,这里返回的是 num_tasks * batch * units 这个维度。
final_outputs.append(sum(weighted_expert_output, axis=2))
# 返回的矩阵维度 num_tasks * batch * units
# 返回多个门控,每个门控有综合多个专家返回的维度 units
# 这里 final_outputs返回的是个list,元素个数等于 门控个数也等于任务个数
return final_outputs
def init_args():
parser=argparse.ArgumentParser(description='dnn_demo')
parser.add_argument("--mode", default="train")
parser.add_argument("--train_data_dir")
parser.add_argument("--model_output_dir")
parser.add_argument("--cur_date")
parser.add_argument("--log", default="https://www.zhihu.com/log/tensorboard")
parser.add_argument('--use_gpu', default=False, type=bool)
args=parser.parse_args()
return args
def get_feature_column_map():
key_hash_size_map={
"adid": 10000,
"site_id": 10000,
"site_domain": 10000,
"site_category": 10000,
"app_id": 10000,
"app_domain": 10000,
"app_category": 1000,
"device_id": 1000,
"device_ip": 10000,
"device_type": 10,
"device_conn_type": 10,
}
feature_column_map=dict()
for key, value in key_hash_size_map.items():
feature_column_map.update({key: tf.feature_column.categorical_column_with_hash_bucket(
key, hash_bucket_size=value, dtype=tf.string)})
return feature_column_map
def build_embeding():
feature_map=get_feature_column_map()
feature_inputs_list=[]
def get_field_emb(categorical_col_key, emb_size=16, input_shape=(1,)):
# print(categorical_col_key)
embed_col=tf.feature_column.embedding_column(feature_map[categorical_col_key], emb_size)
# 层名字不可以相同,不然会报错
dense_feature_layer=tf.keras.layers.DenseFeatures(embed_col, name=categorical_col_key + "_emb2dense")
feature_layer_inputs=dict()
# input和DenseFeatures必须要用dict来存和联合使用,深坑啊!!
feature_layer_inputs[categorical_col_key]=tf.keras.Input(shape=(1,), dtype=tf.dtypes.string,
name=categorical_col_key)
# 保存供 model input 使用.
feature_inputs_list.append(feature_layer_inputs[categorical_col_key])
return dense_feature_layer(feature_layer_inputs)
embeding_map={}
for key, value in feature_map.items():
# print("key:" + key)
embeding_map.update({key: get_field_emb(key)})
return embeding_map, feature_inputs_list
def build_dnn_net(net, params_conf, name="ctr"):
# 可以在下面接入残差网络
for i, dnn_hidden_size in enumerate(params_conf.DNN_HIDDEN_SIZES): # DNN_HIDDEN_SIZES=[512, 128, 64]
net=tf.keras.layers.Dense(dnn_hidden_size, activation="relu", name="overall_dense_%s_%s" % (i, name))(net)
return net
def build_model(emb_map, inputs_list):
# 需要特殊处理和交叉的特征,以及需要短接残差的特征,可以单独拿出来
define_list=[]
adid_emb=emb_map["adid"]
device_id_emd=emb_map["device_id"]
ad_x_device=tf.multiply(adid_emb, device_id_emd)
define_list.append(ad_x_device)
# 直接可以拼接的特征
common_list=[]
for key, value in emb_map.items():
common_list.append(value)
# embeding contact
net=tf.keras.layers.concatenate(define_list + common_list)
# Set up MMoE layer
# 返回的矩阵维度 num_tasks * batch * units
# 返回多个门控,每个门控有综合多个专家返回的维度 units
# 这里 final_outputs返回的是个list,元素个数等于 门控个数也等于任务个数
mmoe_layers=MMoE(units=4, num_experts=8, num_tasks=2)(net)
output_layers=[]
# Build tower layer from MMoE layer
# 对每个 mmoe layer, 后面均接着 2层dense 到输出,
# list,元素个数等于 门控个数也等于任务个数
for index, task_layer in enumerate(mmoe_layers):
# 对当前task, batch * units 维度的数据, 介入隐藏层
tower_layer=layers.Dense(units=8, activation='relu', kernel_initializer=VarianceScaling())(task_layer)
# 这里unit为1,当前任务为2分类
output_layer=layers.Dense(units=1, name="task_%s" % (index), activation='sigmoid',
kernel_initializer=VarianceScaling())(tower_layer)
output_layers.append(output_layer)
# Compile model
# 这里定义了模型骨架,input 为模型输入参数,而output_layers 是一个列表,列表里返回了2个任务各自的logit
# 其实分别返回了每个task的logit,logit这里为分类数目维度的数组,2维过softmax
model=Model(inputs=[inputs_list], outputs=output_layers)
return model
def train():
output_root_dir="{}/{}/{}".format(params_conf.BASE_DIR, args.model_output_dir, args.cur_date)
os.mkdir(output_root_dir)
model_full_output_dir=os.path.join(output_root_dir, "model_savedmodel")
# print info log
log_util.info("model_output_dir: %s" % model_full_output_dir)
# 重置keras的状态
tf.keras.backend.clear_session()
log_util.info("start train...")
train_date_list=DateHelper.get_date_range(DateHelper.get_date(-1, args.cur_date),
DateHelper.get_date(0, args.cur_date))
train_date_list.reverse()
print("train_date_list:" + ",".join(train_date_list))
# load data from tf.data,兼容csv 和 tf_record
train_set, test_set=data_consumer.get_dataset(args.train_data_dir, train_date_list,
get_feature_column_map().values())
# train_x, train_y=train_set
log_util.info("get train data finish ...")
emb_map, feature_inputs_list=build_embeding()
log_util.info("build embeding finish...")
# 构建模型
model=build_model(emb_map, feature_inputs_list)
log_util.info("build model finish...")
def my_sparse_categorical_crossentropy(y_true, y_pred):
return tf.keras.sparse_categorical_crossentropy(y_true, y_pred, from_logits=True)
opt=tf.keras.optimizers.Adam(params_conf.LEARNING_RATE)
# 注意这里设定了2个损失分别对应[ctr_pred, ctcvr_pred]这两个任务
# loss_weights=[1.0, 1.0]这种方式可以固定的调整2个任务的loss权重。
model.compile(
optimizer=opt,
loss={'task_0': 'binary_crossentropy', 'task_1': 'binary_crossentropy'},
loss_weights=[1.0, 1.0],
metrics=[
tf.keras.metrics.AUC(),
tf.keras.metrics.BinaryAccuracy(),
tf.keras.metrics.Recall(),
tf.keras.metrics.Precision()]
)
model.summary()
# tf.keras.utils.plot_model(model, 'multi_input_and_output_model.png', show_shapes=True, dpi=150)
print("start training")
# 需要设置profile_batch=0,tensorboard页面才会一直保持更新
tensorboard_callback=tf.keras.callbacks.TensorBoard(
log_dir=args.log,
histogram_freq=1,
write_graph=True,
update_freq=params_conf.BATCH_SIZE * 200,
embeddings_freq=1,
profile_batch=0)
# 定义衰减式学习率
class LearningRateExponentialDecay:
def __init__(self, initial_learning_rate, decay_epochs, decay_rate):
self.initial_learning_rate=initial_learning_rate
self.decay_epochs=decay_epochs
self.decay_rate=decay_rate
def __call__(self, epoch):
dtype=type(self.initial_learning_rate)
decay_epochs=np.array(self.decay_epochs).astype(dtype)
decay_rate=np.array(self.decay_rate).astype(dtype)
epoch=np.array(epoch).astype(dtype)
p=epoch / decay_epochs
lr=self.initial_learning_rate * np.power(decay_rate, p)
return lr
lr_schedule=LearningRateExponentialDecay(
params_conf.INIT_LR, params_conf.LR_DECAY_EPOCHS, params_conf.LR_DECAY_RATE)
# 该回调函数是学习率调度器
lr_schedule_callback=tf.keras.callbacks.LearningRateScheduler(lr_schedule, verbose=1)
# 训练
# 注意这里的train_set 可以使用for循环迭代,tf 2.0默认支持eager模式
# 这里的train_set 包含两部分,第一部分是feature,第二部分是label ( click, click & conversion)
# 注意这里是 feature,(click, click & conversion),第二项是tuple,不能是数组或列表[],不然报数据维度不对,坑死爹了。
model.fit(
train_set,
# train_set["labels"],
# validation_data=test_set,
epochs=params_conf.NUM_EPOCHS, # NUM_EPOCHS=10
steps_per_epoch=params_conf.STEPS_PER_EPHCH,
# validation_steps=params_conf.VALIDATION_STEPS,
#
# callbacks=[tensorboard_callback, lr_schedule_callback]
)
# 模型保存
tf.keras.models.save_model(model, model_full_output_dir)
# tf.saved_model.save(model, model_full_output_dir)
print("save saved_model success")
if __name__=="__main__":
print(tf.__version__)
tf.compat.v1.disable_eager_execution()
# run tensorboard:
# tensorboard --port=8008 --host=localhost --logdir=https://www.zhihu.com/log
args=init_args()
if args.mode=="train":
train()
到这里,多任务学习之mmoe理论详解与实践就写完成了,欢迎留言交流 ~
宅男民工码字不易,你的关注是我持续输出的最大动力!!!
接下来作者会继续分享学习与工作中一些有用的、有意思的内容,点点手指头支持一下吧~
欢迎扫码关注作者的公众号: 算法全栈之路
- END -
多目标模型成为业界主流有年头了,它凭什么成为业界标配,在成为业界标配的路上,它是如何一步步自我升级从简到繁,本文稍作总结。
详细介绍戳《多目标 | 概览》。
多目标成为业界主流,一方面凭借它自身“多”的实力,另一方面也得益于推荐领域的日渐成熟和“卷”。就像一个人能成功,离不开自身的努力,更离不开时代的浪潮。
各大公司的推荐业务,跟着移动端的普及阶段,在15年前后享受了长时间的红利期。这个阶段,搭乘着用户自然增长的东风,即使推荐系统粗糙,也不妨碍业务的持续增长,工程师对推荐系统做一些显而易见的改进,就可以带来明显的提升效果,所以模型的精细化也没有那么迫切。
随着用户自然增长红利逐渐消失,各大公司的推荐业务也相继进入到存量阶段,这个阶段不再像增量阶段那样,做一些简单的改进很难再带来明显收益,所以“卷”起来了,为了吸引存量的用户在自己的业务场景多花时间,工程师朝着模型精细化的方向进行优化。
单个目标做得好,不能很好地满足业务增长的需要了。比如以点击率为目标建模,对用户点击预估准确,用户很可能会点击,但由于缺乏其它行为的建模,用户点击后的消费时长、和作者的互动等消费难以保证,很可能受标题党、封面党的影响点击了但很快退出了,这种情况下,单目标建模的准确性,并不能很好地表示用户的兴趣。用户不同的行为背后有不同的动机,代表了不同维度的兴趣点。用户点击表示有意愿消费,用户停留一定时长表示有兴趣,用户评论表示愿意和内容生产者产生联系等,一项内容如果能引发用户的正向行为越多,那用户对这项内容的兴趣也越高。当只使用单目标时,很容易导致触发用户某种行为的内容占主导,而忽略了用户背后真实的兴趣,难以保证用户的深度消费,内容分发效果打折,因此,多目标应运而生。
多目标的能力体现在“多”上,光满足用户一种兴趣偏好不能让用户持续性消费,那就满足用户更多的兴趣,满足用户“既要又要”的心理,兼顾更多的方面,变得更懂用户。如果说单目标模型是偏科型选手,那多目标模型就是全科型选手,而这种全科能力恰恰是业务在存量阶段面对增长压力所需要的,优势一目了然,凭实力成为业界标配。
多目标的实力是“多”带来的,但这也带来了挑战:数量从单一变成多个之后,目标之间的关系变得复杂,容易出现“损人利己”的现象,也就是一个目标能力的提高可能会损害其它目标的能力,甚至是损害其它目标效果也无法带来本目标的效果提升,目标之间存在拉扯和跷跷板现象。因此如何缓解多目标学习的跷跷板现象和拉扯,做到大家好才是真的好,是多目标学习的难点。
2.1.1 相关性
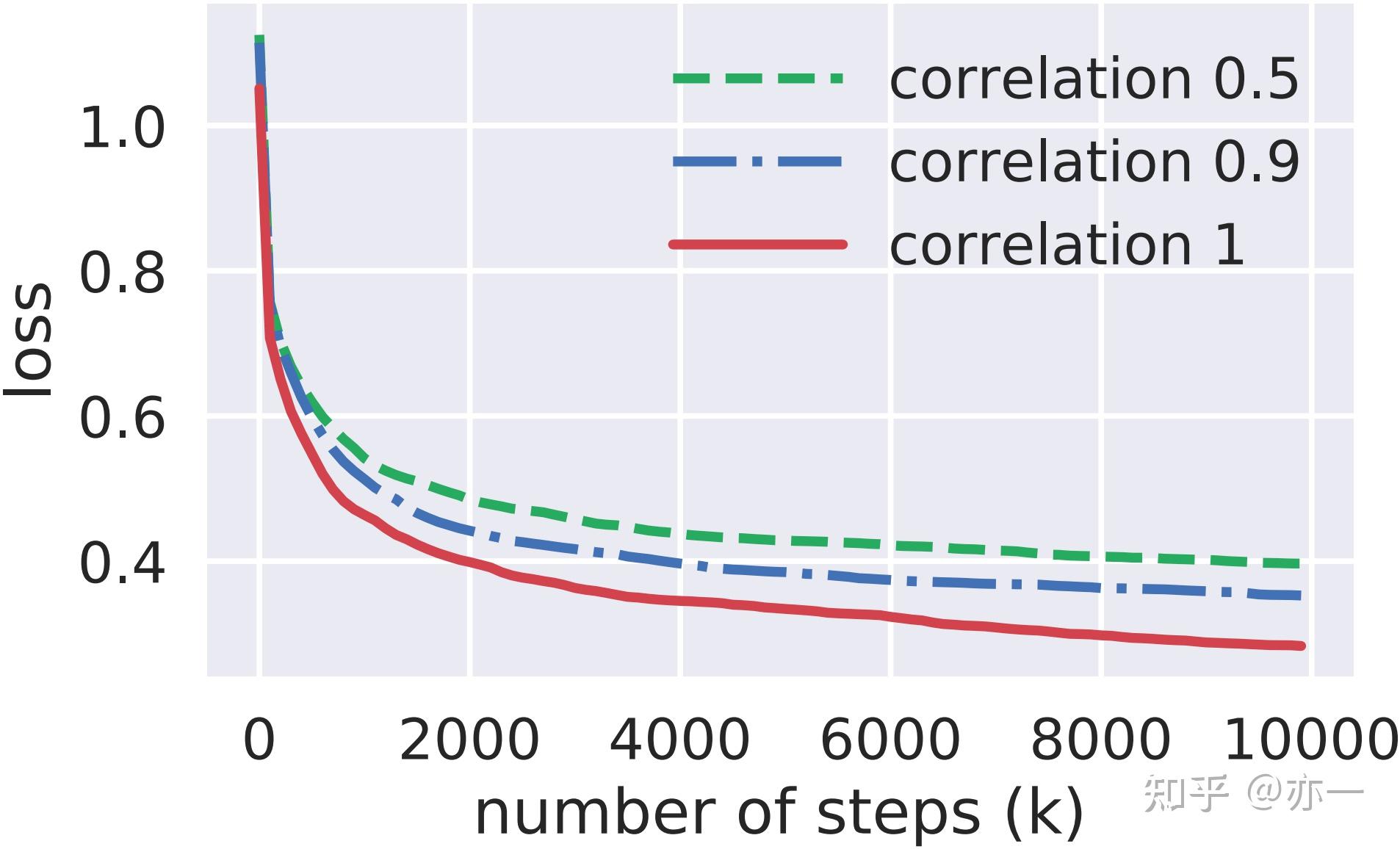
任务之间的相关性直接影响模型的学习效果。当不同task是强相关时,模型学习方向的一致性高,沿着某个方向学习,可以给各个task带来提升,容易形成彼此促进的效果,你好我也好。当task之间的相关性弱,模型沿着某个方向学习,可能能促进某些task而无法促进另一些task的学习,模型的整体效果未必是增强的。论文[1]通过人工生成的数据集对任务相关性和模型效果进行了实验验证,结果如图1所示,模型整体损失随着任务相关性减小而增大,一定程度表示了模型的整体效果随之变弱。
2.1.2 负迁移
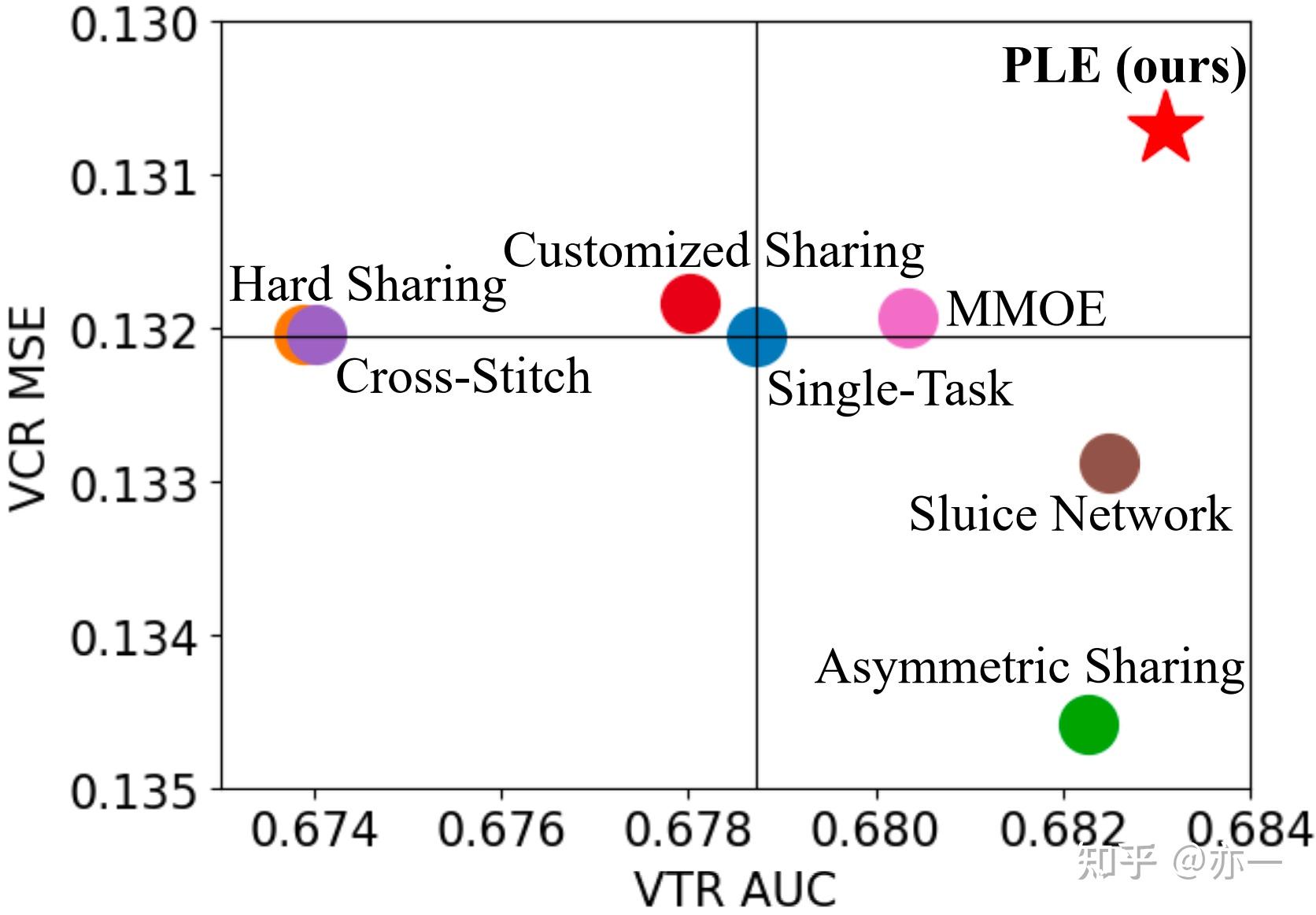
任务之间的复杂关系使得多目标学习容易出现负迁移和跷跷板现象。由于任务之间学习的收敛方向存在不一致的情况,当模型对某个任务学到的信息是正向的,可能对其它任务是负向的,导致效果的负迁移和跷跷板,无法同时提高多个任务的效果。图2[2]表示了多目标模型负迁移和跷跷板现象,即相比于单个任务学习,多目标模型的方法出现一个任务效果下降,另一个任务效果持平或提升的现象。
多目标学习的难度归根结底是因为任务差异性带来的,模型朝着某个方向的收敛难以兼顾所有任务,业界的解决思路从两方面出发:
本文先分享模型结构这种思路的演进路线,后续有机会总结第二种思路。
多目标模型结构的演进,从朴素思路出发,一步步由简到繁,终极目的是提高模型的性价比,用尽可能少的资源得到尽可能好的效果。最开始是训练多个单目标模型,进行组合,然后发展成hard-share的结构。再基于此,衍生出两条优化路线,一条是优化信息表征,这条路线包括mmoe[1], cgc[2], ple[2], fdn[3]等结构,一条是挖掘任务的关系,这条路线包括ESMM[4],ESM2[5]等结构。
多个单目标模型是最朴素的思路,也是最早使用的方法。既然要训多个目标,那每个目标对应一个模型,再对各个单目标模型的结果进行融合,即可实现多目标。
这种方式出发点简单,目标之间互不干扰,没有任务的拉扯问题和负迁移的问题。
它的缺点也很明显:
为了降低多个单目标模型的成本,同时发挥多个目标样本的信息优势,模型朝着hard-share的结构改进。
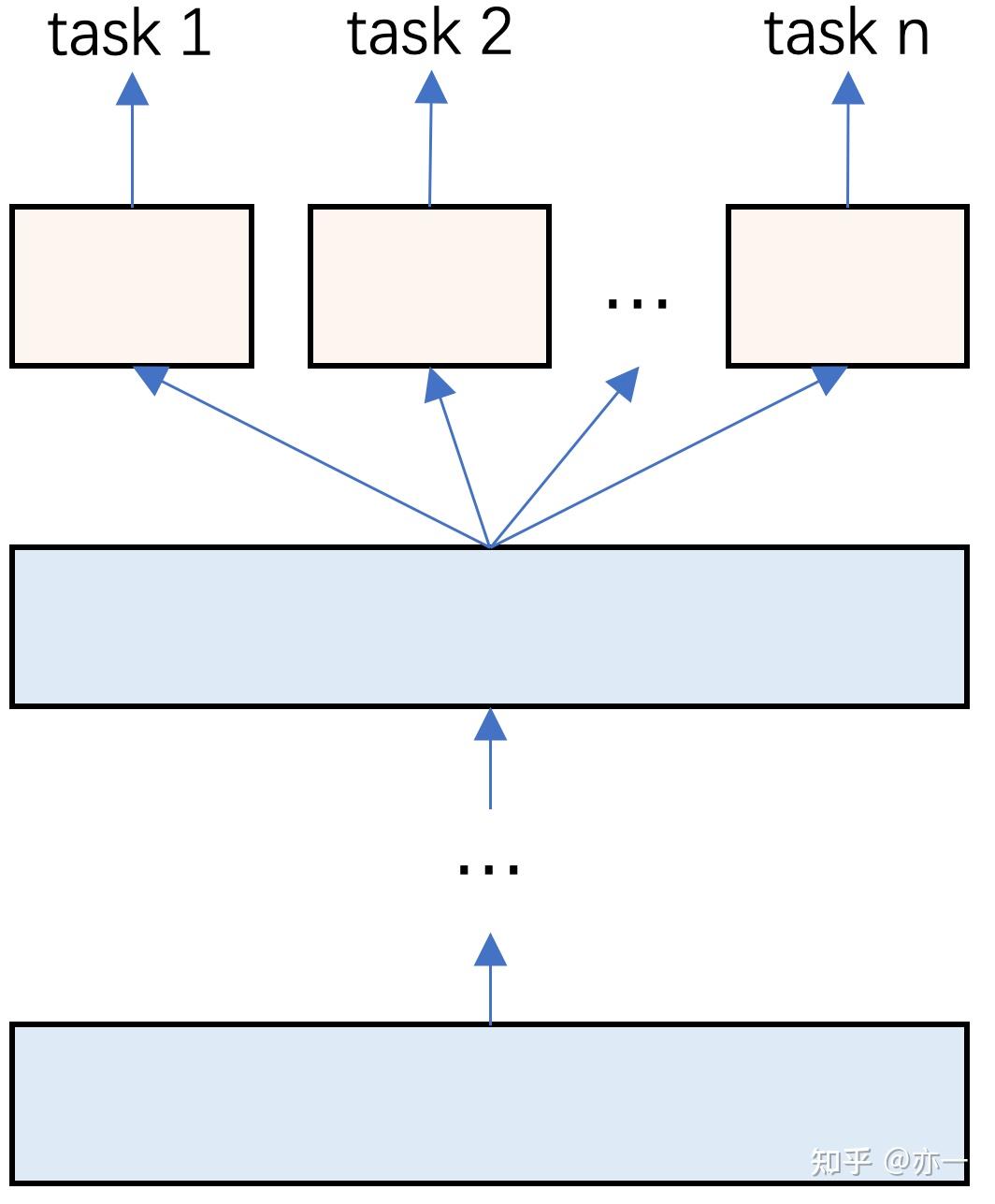
hard-share的模型结构如图3所示,不同任务共享底层输入的embedding输入或部分dense网络,每个task有各自的task网络参数。最小程度的共享,是只共享输入的emebdding,每个task的网络参数独有。在共享embedding的基础上,可以通过对每个task独有的网络dense层引入一些约束,即图3中横向箭头所示,加强共享程度。再进一步的共享可表示为图4,即部分dense层也共享,更高层的dense即为每个task独有的网络。
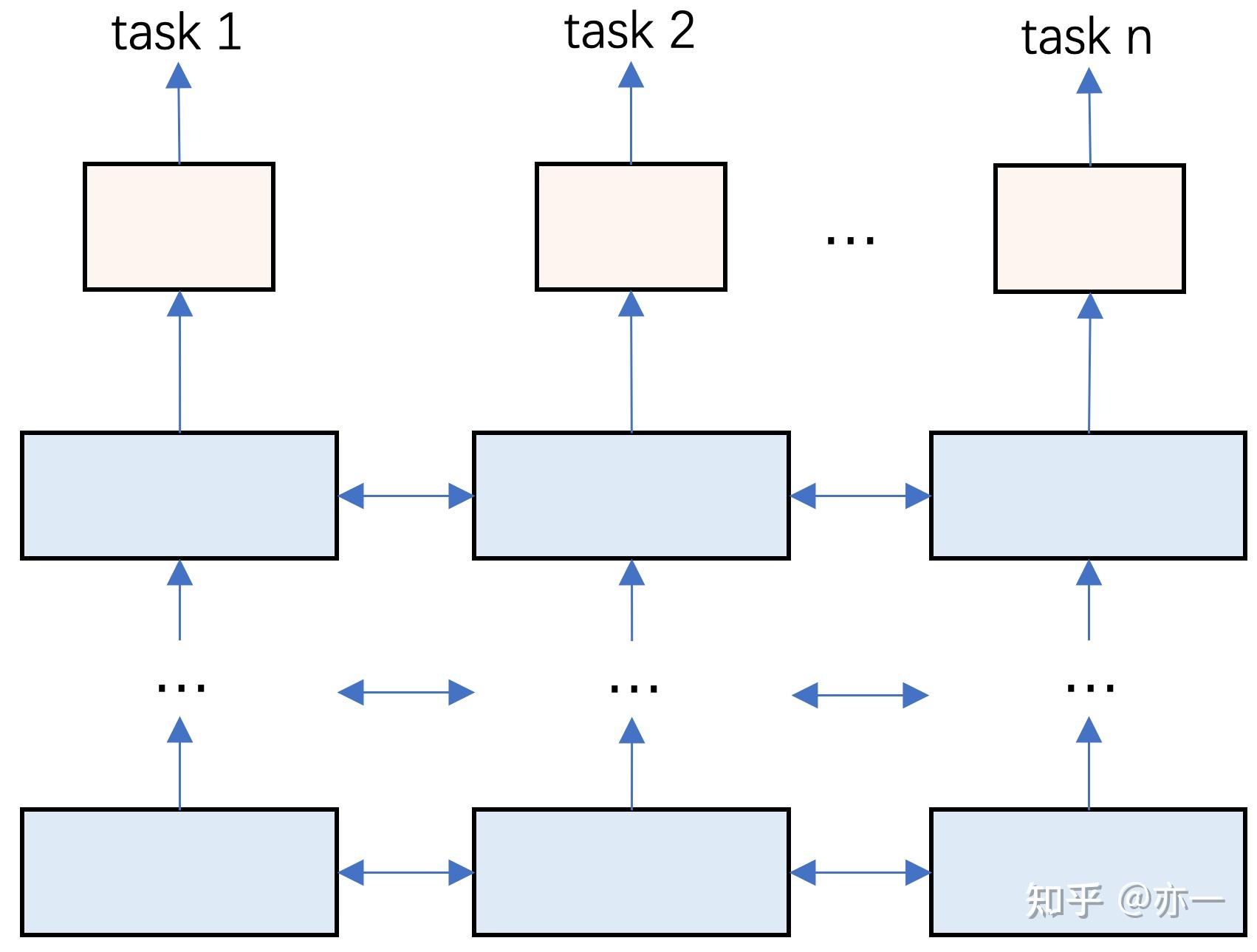
hard-share的结构,一方面可以降低模型的维护成本和迭代成本,增加一个目标只需在已有网络的基础上增加对应的task独有部分的网络,模型的优化也无需针对每个task重复操作;另一方面,共享的emebdding和dense部分,不仅可以使不同目标在统一的输入表征空间下学习,还可以加强对多个task的样本信息利用域融合,提高学习效果。
这种结构也存在一些问题,由于task的关系复杂,share在引入信息的同时也带来了噪声,导致task之间的拉扯和负迁移。因此,这种模型结构在早期被使用较多,随着业界模型结构的发展,也逐渐被效果更好的模型结构取代。
hard-share结构中所有task共享底层信息表征,而底层信息无法对每个task进行差异化处理,体现出task的差异性,因此优化信息表征的思路被提出,对信息表征进行拆分,使得基于这表征得到的task输入,既能表征task的共性,又能表示task的特性,和task做到更好的适配,缓解负迁移和跷跷板现象。这种思路最早被MMoE提出,继而发展出CGC和PLE,近期又出现了新的方法FDN。
3.3.1 MMoE
MMoE是首个提出拆分信息表征的方法,实现了task输入的差异化。MMoE将hard-share中的共享结构拆分为若干部分,也就是expert,再通过gate对expert进行自适应组合,得到每个task的输入。通过Gate对expert的自适应组合的方式,task的输入表征兼具task共性和特性,提高了和task的适配性。
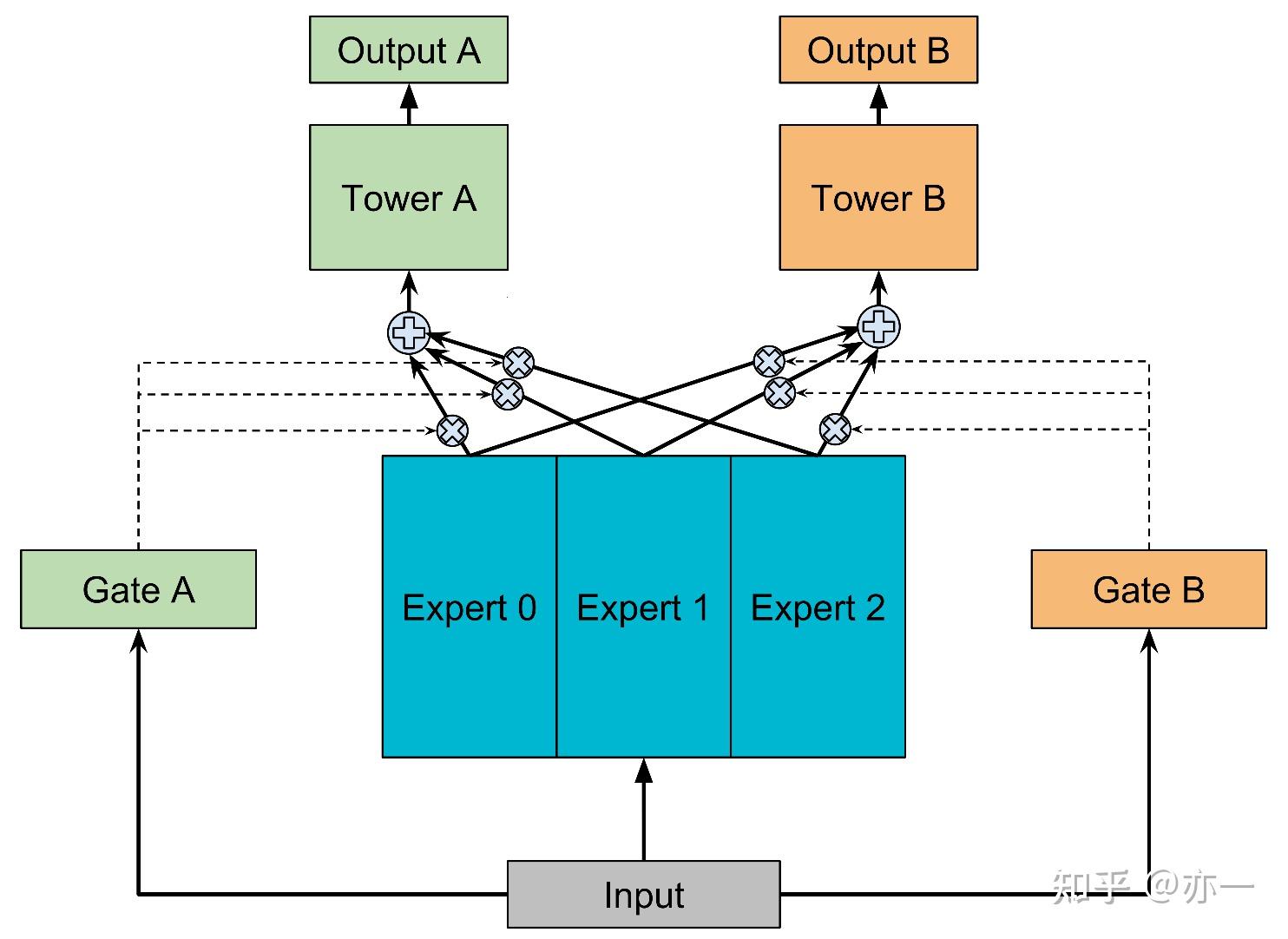
模型结构如图5所示,gate的输入为模型的输入,输出计算如式子(1)所示,expert根据gate输出的权重加权求和,得到task的输入,再进行task的预估,如式子(2)所示。
MMoE拆分信息表征的思路给业界模型结构的优化提供了一个方向,但想在实际应用中取得效果并不容易,容易出现坍缩等现象,需分析模型训练情况并进行针对性改进,具体方法见《多目标 | 模型结构: MMoE实际应用,理论和实践是两回事》。MMoE中信息表征的优化,expert的拆分是task无差别的,因此task的共性和特性的表征的区分,可以进一步加强,因此CGC和PLE的结构被提出。
3.3.2 CGC和PLE
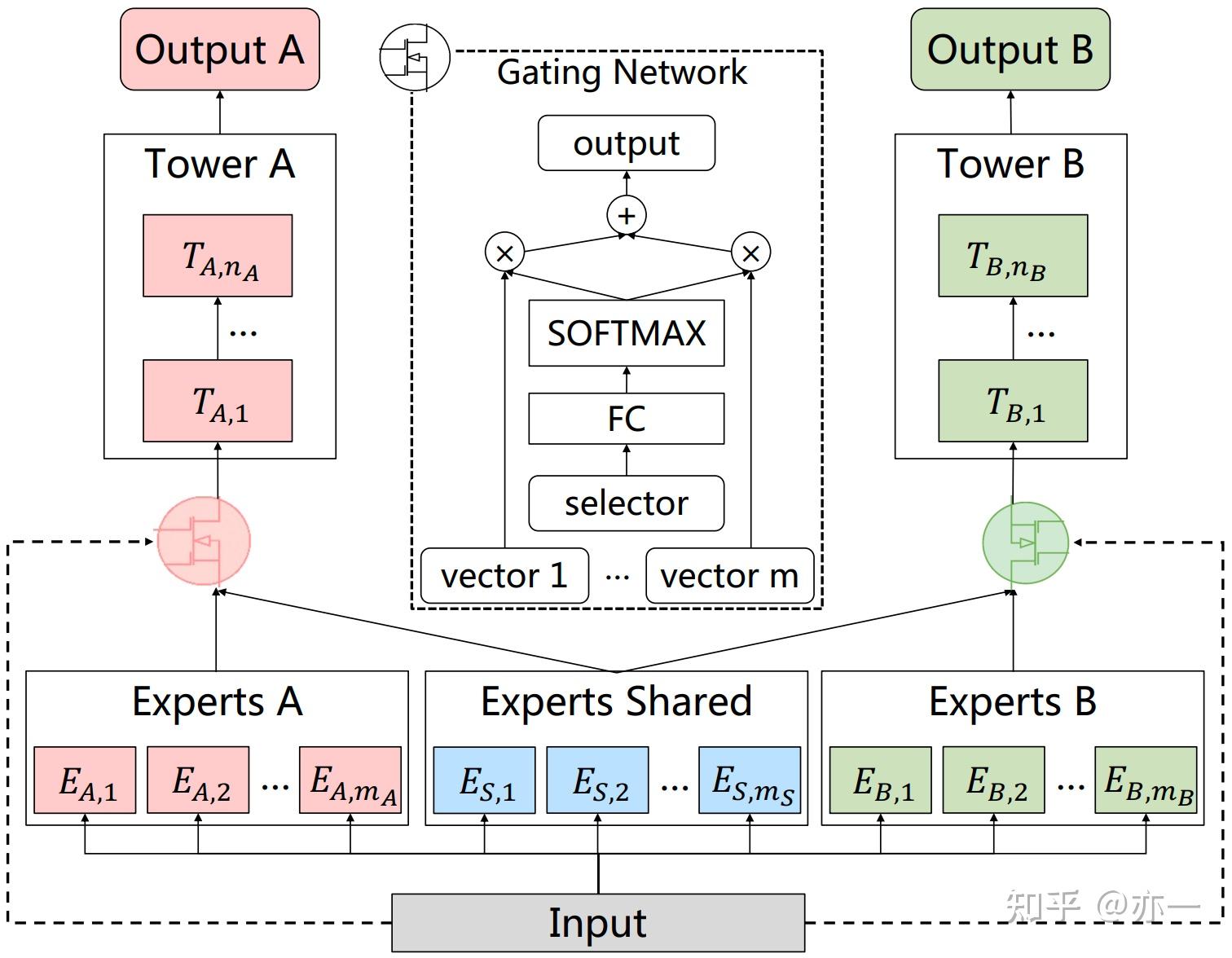
CGC和PLE对信息表征做了更细致和更具区分性地拆分,在信息表征的结构中将expert分为task共享和独有两种,共享expert所有task共享,独有的expert每个task各自独立,task的输入由共享expert和task独有expert经过gate加权组合得到。这种方式提高了expert表征的差异性和对task的针对性,在利用共享信息的同时,减少了其它task的噪声,实现和task更好地适配。CGC是简化版的PLE,CGC利用bottom结构进行信息抽取,当有多层bottom结构时,则为PLE。
CGC模型结构如图6所示。bottom结构中的两种expert,每种可以由多个小expert构成,每个task的输入通过gate对共享expert和独有expert加权组合得到。
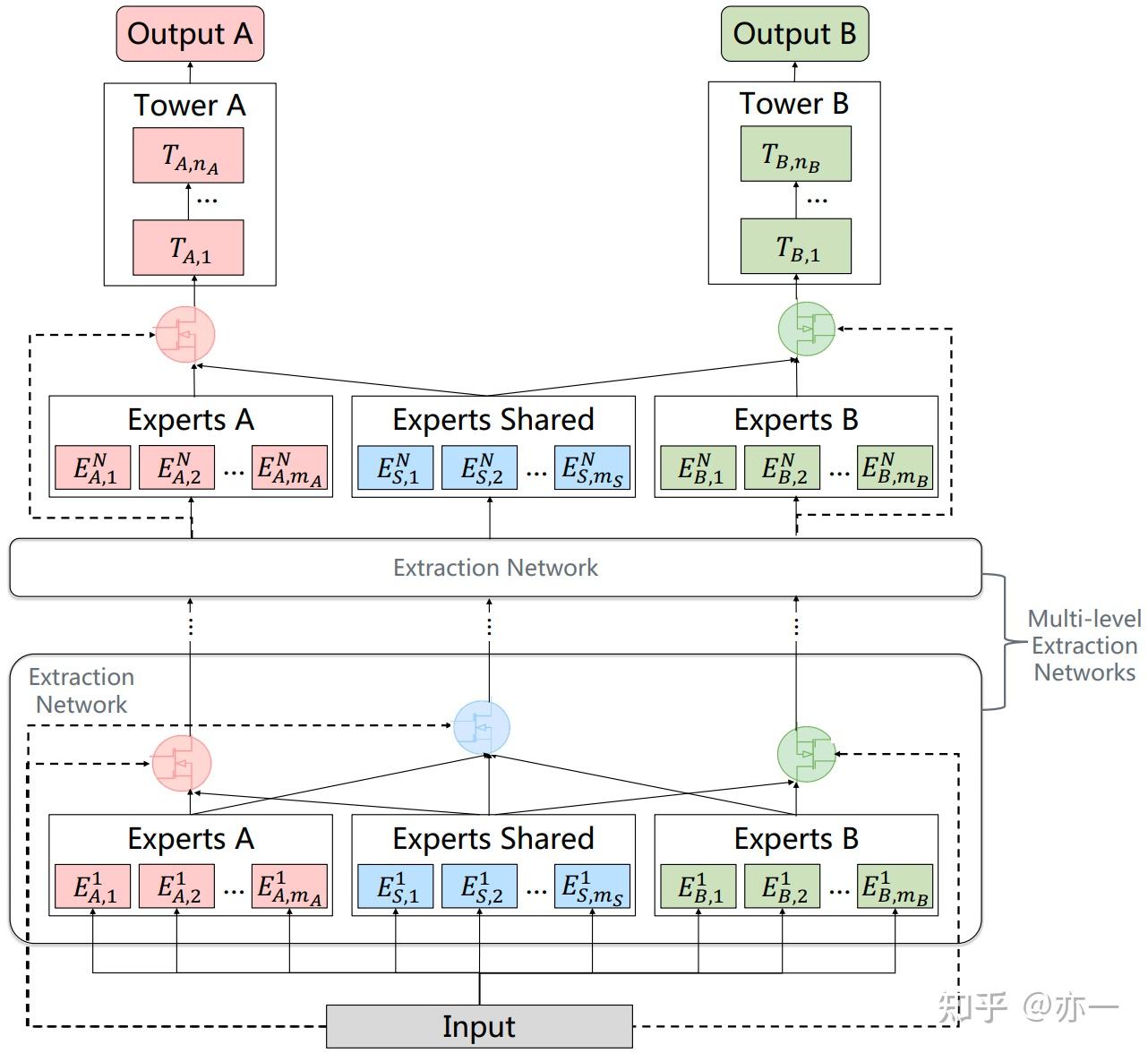
PLE的结构如图7所示,特征提取部分由多个bottom逐层累加,每个bottom中task共享的expert由前一个bottom中所有expert通过gate组合得到,task独有expert由前一个bottom中共享expert和对应task的独有expert通过gate组合得到。
CGC和PLE虽然进行了更有区分性的信息表征提取,但仍然采用自适应地方式组合输入到task中,信息表征在学习过程中受到的约束弱,仅来自task最终的label信号的约束。模型虽然是万能的,但模型也是懒惰的,它会以一种最偷懒地方式学到当前约束下的最优,这种最优跟期待的极有可能存在较大差距。在CGC和PLE中,期待模型学到task共享和独有的信息表征,很可能实际学到的这两种表征差异不大。为了使模型克服惰性,朝着预期的方向学习,需引入更强的约束,因此FDN被提出。
3.3.3 FDN
FDN在CGC思路的基础上,对信息表征的拆分进一步细化和差异化,并对信息表征的学习引入了更强的约束,提高共享和独有的信息表征在空间上的正交性。
模型结构如图8所示,每个task采用单组或多组分解对(DeComposition Pair,简写为DCP),每组分解对包括task共享和task独有两种信息表征。不同于CGC和PLE,FDN中每个task都有该task独立的共享信息表征。每个task的输入由两部分构成,一部分是共享信息表征,由所有task的共享表征融合而成,另一部分是task独有信息表征,这两部分通过gate权重的形式加权组合得到task的输入。
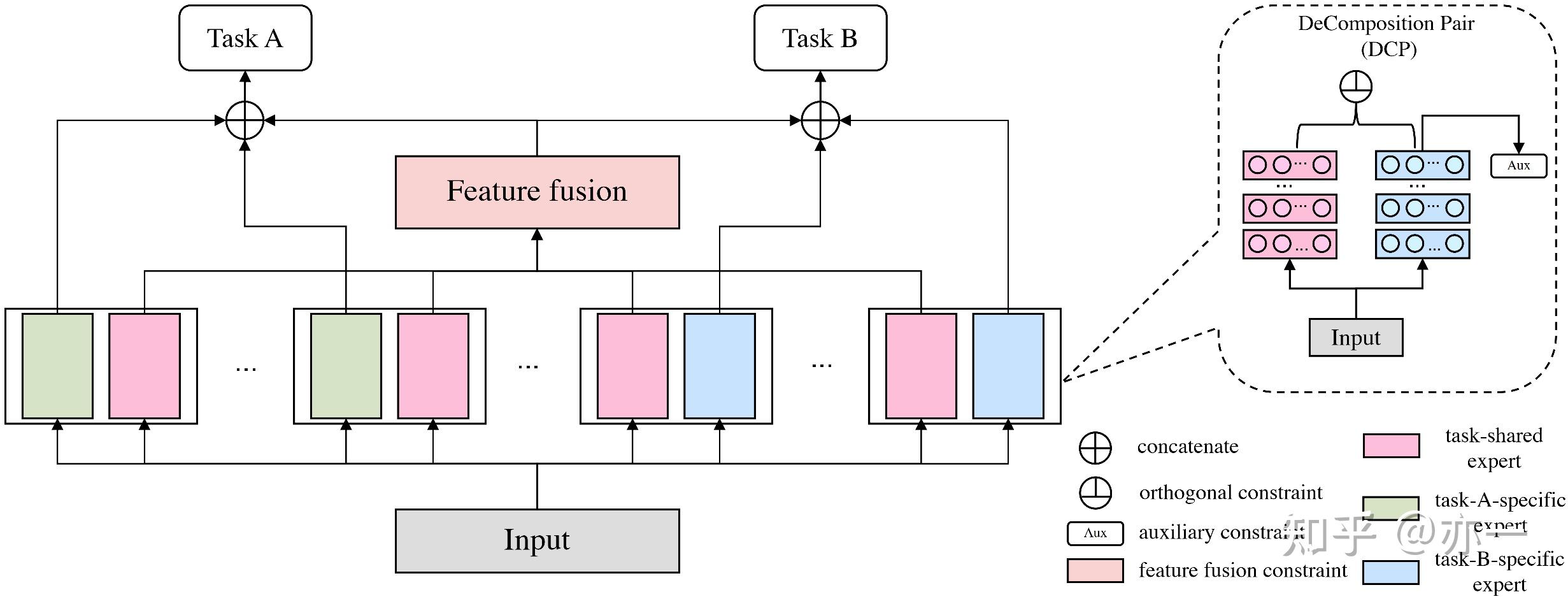
FDN的核心优化不在于信息表征的拆分,而在于对信息表征的学习引入了两种约束,使其受限于更强的监督信号,朝着期望的共享和独有方向收敛。
一种约束是正交约束,使每个task的DCP中共享和独有两种特征表征在空间上形成正交,尽可能差异化,从而提高模型对各个task的共性和差异性的捕捉能力。正交约束的计算如式子(3)所示,其中表表示task k的第m个task共享的特征表征,
表示task k的第m个task独有的特征表征,
为Frobenius范数。
一种是辅助loss约束,将DCP中task独立的特征表征看成是该task特征抽取的单独小网络,用这部分的特征表征进行task预估,作为辅助task,如式子(4)所示,其中task k的辅助loss函数,可以选择和主loss保持一致,
为task k的真实标签,
为task k中第m个独有特征表征的task预估,计算如式子(5)所示。task共享和独有表征的正交子空间有很多,它们不一定能学到task目标所需要的两种子空间上。辅助loss的引入,可以正交的子空间方向,和task的目标保持一致性。
所有task共享特征表征进行融合得到整体的共享表征,可以看做是一种间接的隐式约束,即把各个task的共享表征的学习约束到同一个子空间。
FDN整体的损失包括task的主loss,正交loss和辅助task loss三部分,如式子(6)所示。
FDN对信息表征引入约束,不仅适用于多目标的优化,属于一种通用的模型优化方向,用于改善模型的惰性。
通过任务之间的依赖关系来改进模型结构,典型的方法包括ESMM和ESM2。这种思路主要是解决训练和推理推理空间不一致的问题,以及间接地缓解样本稀疏的问题。典型的应用场景是电商,利用点击(CTR)和转化(CVR)的行为依赖性,将hard-share的形式改进为级联结构。这种方式不仅限于电商场景,在其它涉及到行为依赖性的场景均适用,比如直播场景中的点击和点击后续行为的目标建模。
数据稀疏
用户在推荐场景产生的行为数据,呈漏斗状,曝光是第一层漏斗,数据最多,接着被点击过滤一层,数据相应地减少,再接着被点击后的如购买、评论等行为过滤一层,数据进一步减少。图9[3]表示了数据从曝光到购买的逐层减少。相比曝光空间(表示为),点击空间(表示为
)数据量通常减少1-3个数量级。对电商场景中的转化行为建模,如果仅使用点击空间的数据,样本将面临稀疏的问题,模型学习难度大。
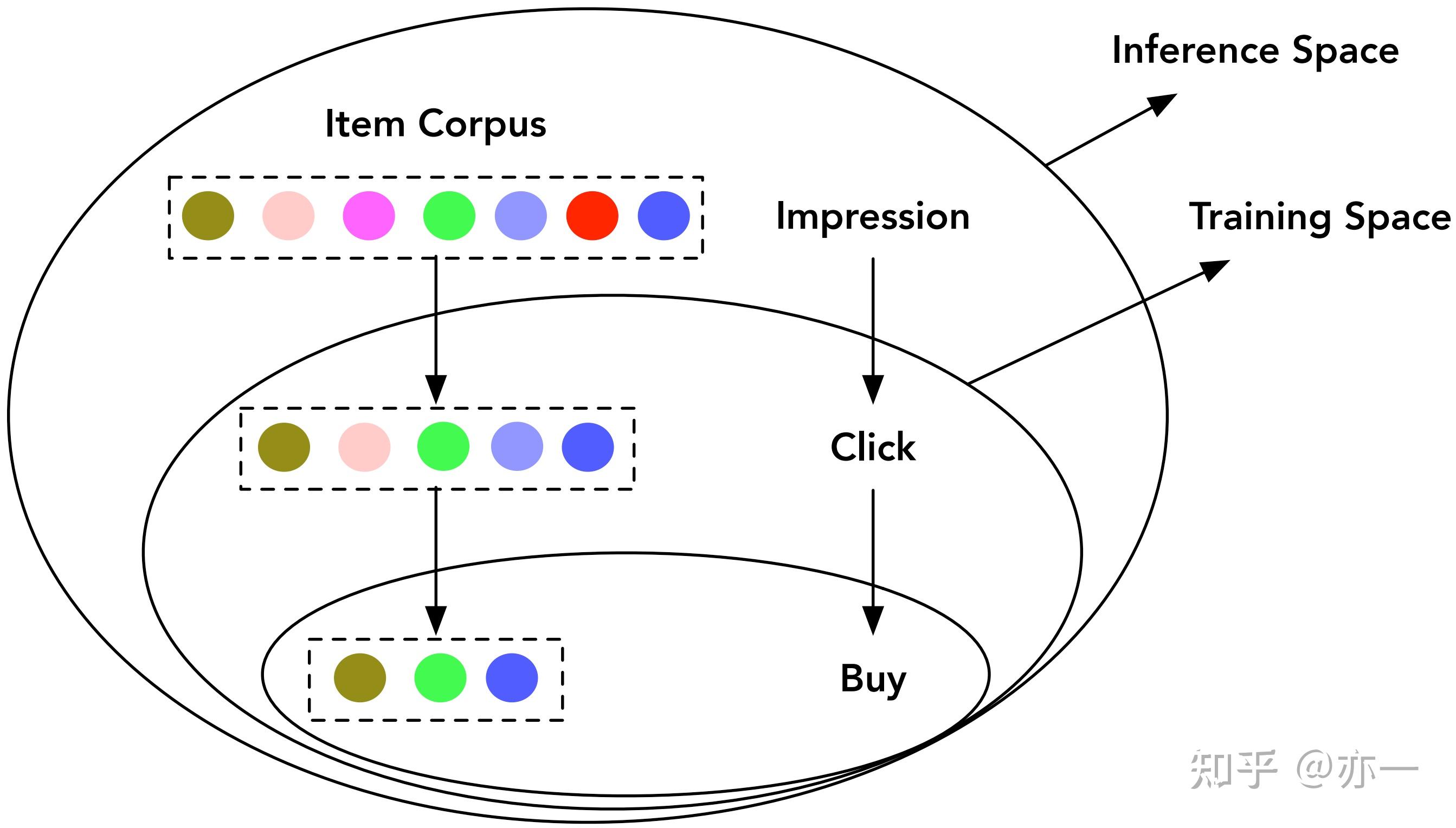
训练和推理空间不一致
选择点击空间建模而非曝光空间建模,另一个严重的问题是训练和推理空间不一致的问题,也被称为样本选择偏差(SSB)。模型训练用的是点击空间的样本,但推理是在曝光时刻对用户购买行为进行预估,面对的是曝光空间,点击和曝光空间在数据分布上有明显差异,这违背了机器学习中数据分布一致性的基本假设,导致训练效果好无法泛化到线上推理空间,影响模型线上效果。
训练和推理空间不一致问题,不仅是早期电商场景CVR任务面临的,在粗排模块上也存在类似的问题。粗排的样本选择如果和精排的样本选择保持一致,那么粗排的训练是基于曝光空间,而粗排的推理是在召回结果对应的空间,曝光空间是召回结果的子集。
ESMM和ESM2基于任务依赖关系对模型结构进行级联改进,对task在曝光空间建模,解决了训练和推理空间不一致的问题,同时由于所有样本底层embedding共享,间接地缓解了数据稀疏问题。
3.4.1 ESMM
ESMM利用转化行为对点击行为的依赖性,对CTR和CVR任务进行级联,隐式地将CVR任务的建模空间变成曝光空间,解决了CVR任务在训练和推理空间不一致的问题。
3.4.1.1 模型原理
建模的核心目标是准确地预估用户从物品曝光到购买的概率CTCVR,根据曝光-点击-购买的路径依赖,CTCVR可由CTR*CVR计算得到。ESMM模型结构如图10所示,CTR和CVR级联得到CTCVR。
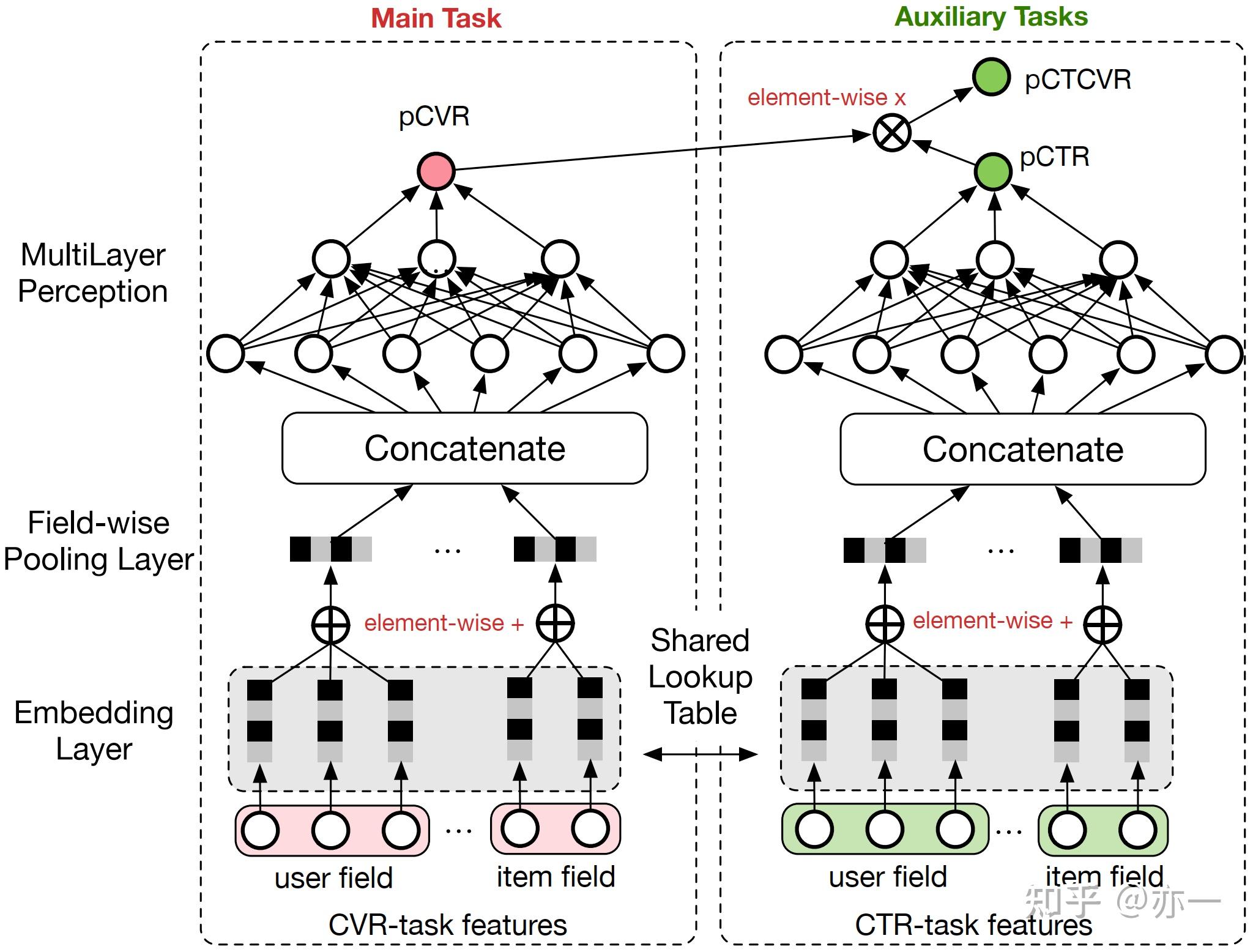
CTCVR的计算如式子(7)所示,其中 表示曝光样本输入特征,
表示发生点击行为,
表示发生购买行为。样本集可以表示为
,
表示样本数量。
损失函数包括CTR和CTCVR损失,这两个任务都是基于曝光样本空间的直接建模,从而实现隐式地基于曝光空间学习CVR任务。损失函数如式子(8)所示,其中 和
表示CTR和CVR任务的参数,
表示交叉熵损失。
3.4.1.2 模型分析
模型对CTR和CTCVR任务的直接学习,这两个任务均是在曝光样本空间进行,因此相当于使CVR任务在曝光样本空间间接学习,从而解决了样本选择偏差问题。
3.4.2 ESM2
ESM2是ESMM的升级版,根据行为的依赖性建模,对行为依赖路径进行了更细化的拆分。
3.4.2.1 路径拆分
ESM2在ESMM的基础上,在点击和转化之间加入了一个中间行为,即有无特定行为,特定行为包括决定性行为和其它行为,行为路径的抽象过程如图11所示,从图11(a)逐步抽象到图11(c)所示,最终将行为路径表示为“曝光-点击-有特定行为/无特定行为-购买”。从曝光到转化的概率,由该行为路径上每个阶段对应的概率相乘得到。
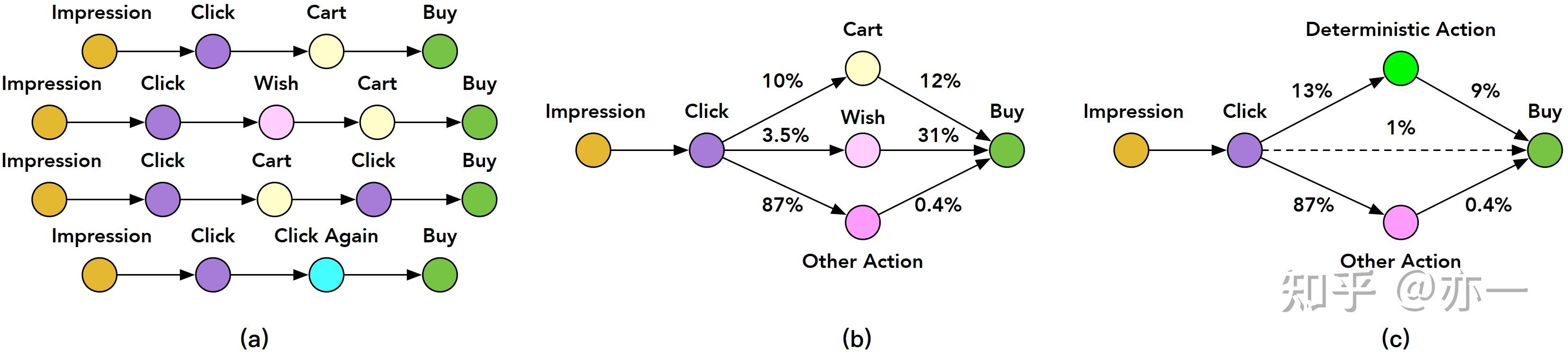
3.4.2.1.1 CTAVR
CTAVR表示从曝光到产生特定行为的转化,计算过程如式子(9)所示,其中表示曝光,值为1,
表示点击行为,值为1时表示点击行为发生,值为0时表示点击行为未发生,
表示特定行为,值为1时表示特定行为发生,值为0时表示特定行为未发生。当点击行为未发生时,后续行为无法产生,因此
。
3.4.2.1.2 CVR
CVR表示从点击到购买的转化,计算过程如式子(10)所示,其中表示购买行为,值为1时表示购买行为发生,值为0时表示购买行为未发生。在用户行为路径上,购买行为的前置依赖行为包括两种情况:有特定行为和无特定行为,因此
。
3.4.2.1.3 CTCVR
CTCVR表示从曝光到购买的转化,计算过程如式子(11)所示,由是否有特定行为两种情况下对应的曝光到购买的转化概率相加得到。
3.4.2.2 模型结构
ESM2的模型结构如图12所示,对用户行为路径上存在依赖关系的任务进行级联。模型包括三部分:embedding共享模块(SEM),预测分解模块(DPM)和序列行为合成模块(SCM)。
SEM模块通过任务共享底层embedding,使模型充分利用样本量大的任务进行学习,间接缓解数据稀疏问题。
DPM模块根据用户行为路径,将曝光到购买的整个过程分解为4部分,从曝光到点击,从点击到有特定行为,从有特定行为到购买,从无特定行为到购买,每部分进行相应的建模。
SCM模块根据行为之间的依赖性和DPM模块中已有的分解过程,对任务进行级联,CTR, CTAVR, CTCVR均是基于曝光样本空间,从而实现CVR任务基于曝光空间的间接建模,保证了训练和推理的空间一致性。
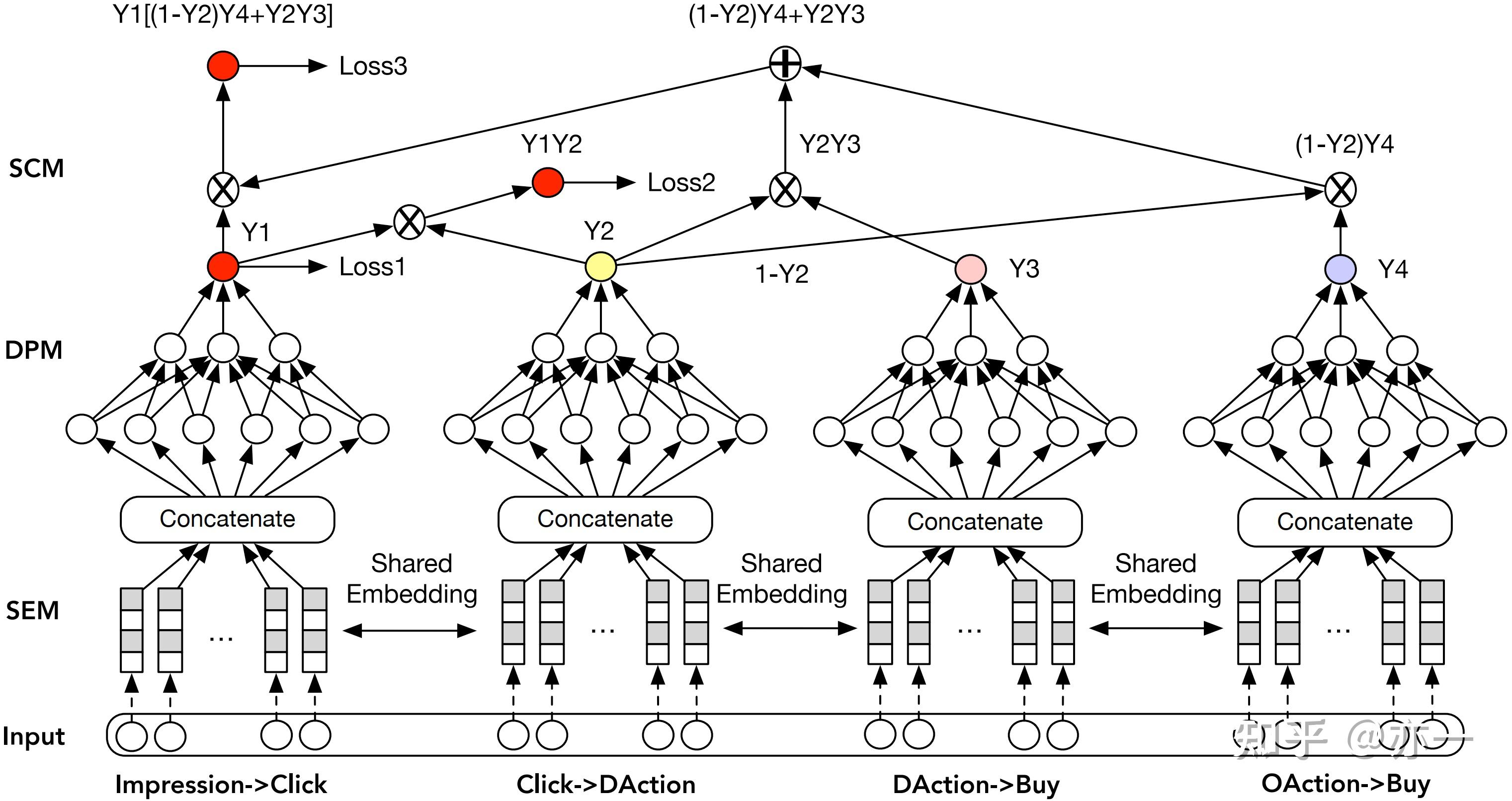
3.4.2.3 损失函数
ESM2的损失由这CTR、CTAVR和CTCVR三个任务的损失构成,分别如别如式子(12)(13)(14)所示,其中,C表示点击行为空间,A表示特定行为空间,B表示购买行为空间,+表示正样本,-表示负样本。整体损失由这三分部加权求和得到,如式子(15)所示。
多目标模型结构优化的以上两个方向,是两个不同的维度,对模型来说,两者不冲突,可以在应用中结合使用。多目标在模型结构上发展方向,后续大概率还会沿着这两个方向继续,但目前肉眼可见两个方向难以实现亮眼的突破,希望未来可以见到一些亮眼的工作。
reference
[1]Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts. https://dl.acm.org/doi/pdf/10.1145/3219819.3220007
[2]PLE Progressive Layered Extraction (PLE): A Novel Multi-Task Learning (MTL) Model for Personalized Recommendations. https://dl.acm.org/doi/abs/10.1145/3383313.3412236
[3]Feature Decomposition for Reducing Negative Transfer: A Novel Multi-task Learning Method for Recommender System. Feature Decomposition for Reducing Negative Transfer: A Novel Multi-task Learning Method for Recommender System
[4]Entire Space Multi-Task Model: An Effective Approach for Estimating Post-Click Conversion Rate. Entire Space Multi-Task Model: An Effective Approach for Estimating Post-Click Conversion Rate
[5]Entire Space Multi-Task Modeling via Post-Click Behavior Decomposition for Conversion Rate Prediction.Entire Space Multi-Task Modeling via Post-Click Behavior Decomposition for Conversion Rate Prediction
多目标系列
推荐系列文章:
【播播笔记】公众号分享推荐主业,欢迎关注
【吾之】公众号胡说八道,欢迎关注
金鹰优化算法(Golden eagle optimizer,GEO)由Abdolkarim 等人于2020年提出,该算法模拟了金鹰狩猎行为,具有收敛速度快,寻优能力强的特点。

GEO原理参考博客:智能优化算法:金鹰优化算法-附代码_智能算法研学社(Jack旭)的博客-CSDN博客



MOGEO原理参考文献: Mohammadi-Balani A , MD Nayeri, Azar A , et al. Golden Eagle Optimizer: A nature-inspired metaheuristic algorithm[J]. Computers & Industrial Engineering, 2020, 152:107050.

参考文献: Zhang Q , Zhou A , Zhao S , et al. Multiobjective optimization Test Instances for the CEC 2009 Special Session and Competition[J]. Mechanical engineering (New York, N.Y.: 1919), 2008.

CEC2009中无约束多目标测试集(UF1-UF10)详情如下:




MOGEO求解UF1-10,并利用IGD、GD、HV和SP对其评价,种群大小为100,最大迭代次数200。加大迭代次数和加大种群规模效果更佳。
部分实验结果:
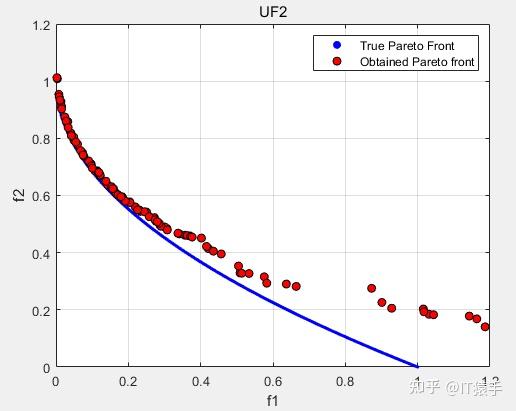
IGD:0.074401
GD:0.0059532
HV:0.63396
SP:0.0117
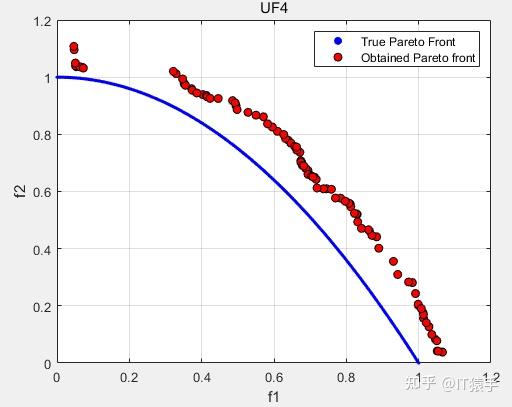
IGD:0.090882
GD:0.0097464
HV:0.32406
SP:0.0084643
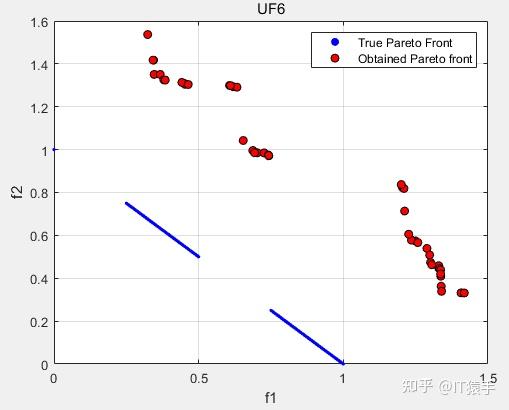
IGD:0.50153
GD:0.082518
HV:0.044862
SP:0.019312
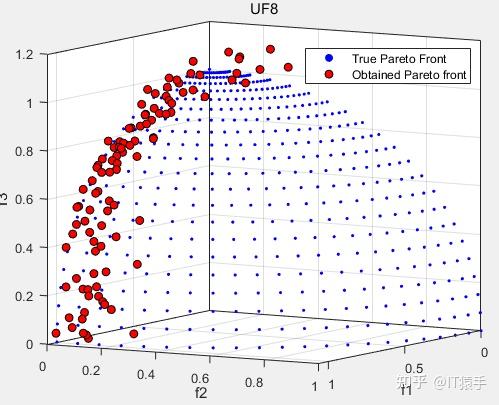
IGD:0.30584
GD:0.0052096
HV:0.30763
SP:0.035375
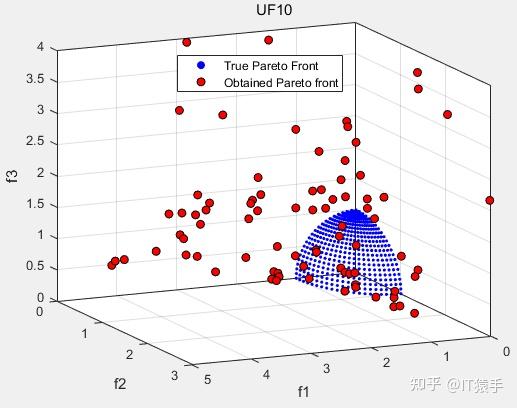
IGD:0.52521
GD:0.18792
HV:0.0026319
SP:0.3134
可以看出MOGEO在多目标问题测试集UF上求解效率较低,改进空间很大。
获取完整MATLAB代码详见博主主页。